안녕하세요 Steve-Lee입니다. 이번 시간부터는 Lecture 6. Training Neural Network에 대해 배워보도록 하겠습니다. Deep Learning Model을 학습시키는 과정에서 저희가 알고 넘어가야 할 기본적인 내용들을 하나하나 살펴보도록 하겠습니다.
모두를 위한 cs231n
모두를 위한 cs231n 😀
👉🏻 시작합니다! 🎈
모두를 위한 cs231n (feat. 모두의 딥러닝 & cs231n)
👉🏻 Neural Network 기초 📗
* Backpropagation
Lecture4. Backpropagation and Neural Network. 오차역전파에 대해서 알아보자😃
👉🏻 Training Neural Network Part I 📑
- Activation Function 파헤치기
Lecture 6. Activation Functions에 대해 알아보자
Lecture 6. Activation Functions - ReLU함수의 모든 것
- Data Preprocessing
Lecture 6. Training Neural Network - Data Preprocessing
- Weight Initialization
Lecture 6. Weight Initialization
- Batch Normalization
Lecture 6. Batch Normalization
👉🏻 Deep Learning CPU와 GPU ⚙️
Lecture 8 - Part1. Deep Learning 을 위한 CPU와 GPU
👉🏻 Deep Learning Framework ☕️
Lecture 8 - Part2. Deep Learning Framework
👉🏻 TensorFlow Fraemwork 🧱
Lecture 8 - Part3. TensorFlow Framework
👉🏻 PyTorch Framework 🔥
Lecture 8 - Part3. PyTorch Framework
👉🏻 Generative Model
모두를 위한 cs231n (feat. 모두의 딥러닝 & cs231n)
cs231n 시작합니다! 안녕하세요. Steve-Lee입니다. 작년 2학기 빅데이터 연합동아리 활동을 하면서 동기, 후배들과 함께 공부했었던 cs231n을 다시 시작하려고 합니다. 제가 공부하면서 느꼈던 점들과
deepinsight.tistory.com
Part I Index
- Activation Functions
- Data Preprocessing
- Weight Initialization
- Batch Normalization
- Babysitting the Learning Process
- Hypperparameter Optimization
Activation Functions
딥러닝 학습을 위해 어떤 Activation Function을 사용할 수 있을까요? Perceptron에서 많이 사용하는 Step Function부터 Linear Activation Function 등 우리가 아는 Activation Function을 사용하면 될까요?
안타깝게도 위의 두 함수는 좋은 Activation Function이 아닙니다.

우선 Step Function은 0과 1 두 값으로 밖에 출력을 할 수 없습니다. 즉 다중 출력을 할 수 없습니다.
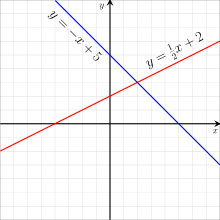
다음으로 Linear Activation Function입니다. Step Function과 달리 다중 출력을 할 수는 있지만 두 가지 문제점을 가지고 있습니다.
첫째, Backpropagation이 불가능합니다. 다음으로 Hidden Layer를 무시하는 결과를 출력합니다. h(x)=cx 일 때, hidden layer를 겹겹이 쌓아도 출력은 c'x로 같기 때문입니다.
오늘은 딥러닝 학습을 위한 6가지 Activation Function에 대해 배워보도록 하겠습니다. cs231n Lecture6. Training Neural Network Part I을 참고하였습니다.
Activation Function이란?
입력 신호의 총합을 출력신호로 변환하는 함수를 일반적으로 Activation Function이라고 합니다.
활성화(Activate)라는 이름에서 알 수 있듯이 활성화 함수란 입력 신호의 총합이 활성화를 일으키는지 정하는 역할을 한다 -밑바닥부터 배우는 딥러닝-
아래의 그림은 Activation function의 Computational Graph(계산 그래프)입니다.
input과 weight의 내적 값에 bias를 더한 값을 얼마나 출력시킬지 정하기 위해 Activation Function을 사용합니다.

6가지 활성화 함수에 대해 알아보자

이번 시간에는 6가지 Activation Function에 대해 배워보도록 하겠습니다.
- Sigmoid
- tanh
- ReLU
- LeakyReLU
- ELU
- Maxout
01. Sigmoid
가장 먼저 Sigmoid 함수가 있습니다.

- 특징
- 출력 값을 0에서 1로 변경해줍니다.(Squashes number to range [0, 1])
- 가장 많이 사용되었던 활성화 함수라고 합니다.
- 단점
- Saturation(포화상태)
- Sigmoid outputs are not zero-centered
Sigmoid 함수의 두 가지 문제점
Sigmoid함수의 두 가지 문제점에 대해 알아보도록 하겠습니다.
Sigmoid 문제점 I
우선 Saturation문제가 있습니다. Saturate라는 의미는 무엇일까?
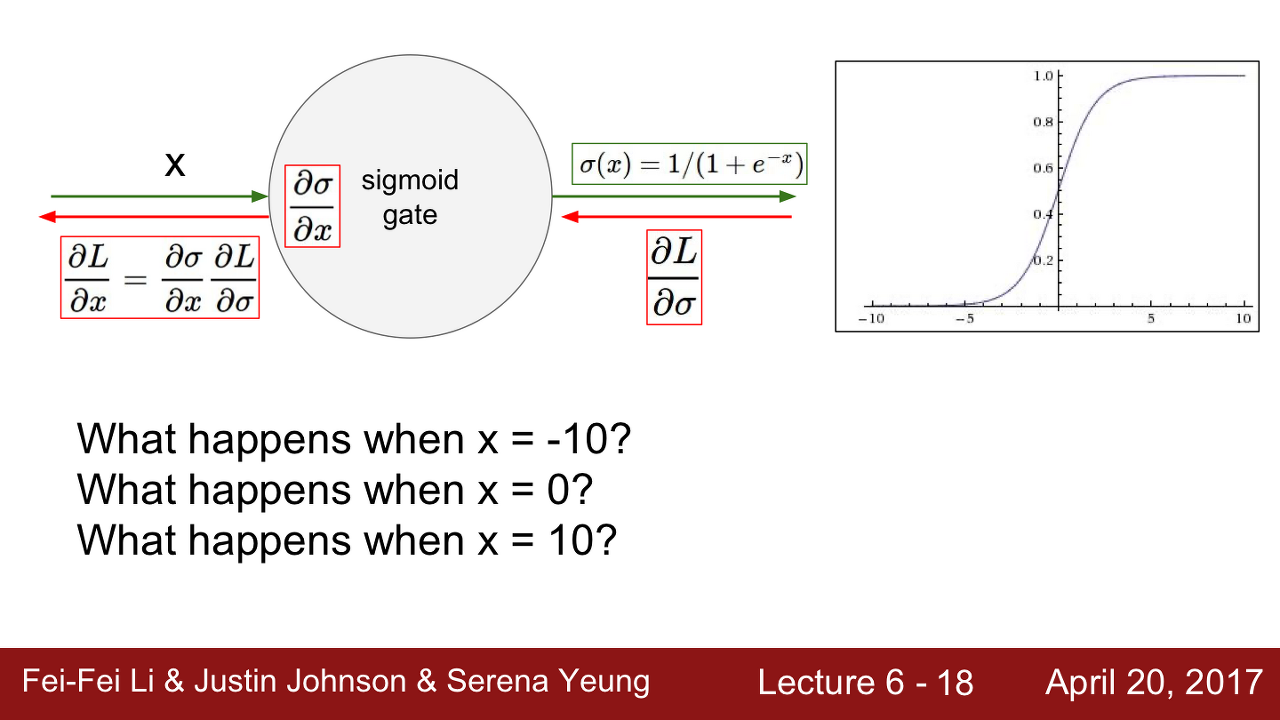
Sigmoid 함수의 출력 그래프를 보면 입력 신호의 총합이 크거나 작을 때 기울기가 0에 가까워지는 것을 볼 수 있습니다. 이렇듯 Activation Function의 구간에서 기울기(gradient)가 0에 가까워지는 현상을 Saturated라고 합니다. 이는 Vanishing Gradient문제를 야기합니다.
Sigmoid 문제점 II
두 번째 문제는 Sigmoid 함수가 zero-centerd 하지 않다는 점입니다.

저는 이 부분이 상당히 많이 헷갈렸습니다. 제가 이해한 대로 한 번 풀어보도록 하겠습니다. -20.05.18.mon-

Q. 만약 neuron의 input값인 x가 항상 양수라면 gradient W는 어떻게 될까요?
A. 항상 양수 이거나/항상 음수 일 것입니다. Computational Graph를 통해 살펴보겠습니다.
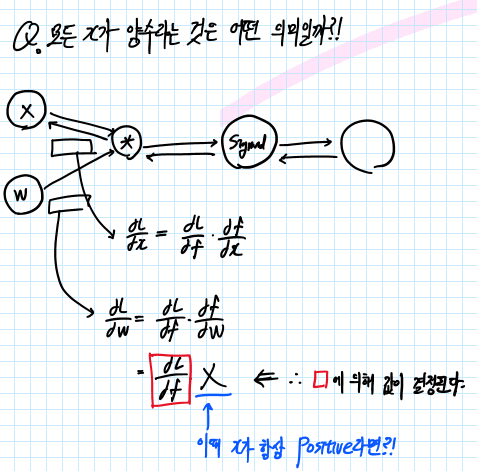
Computational Graph를 그려서 Backprop을 해봅니다.
W의 Gradient를 구하는 과정을 Computational Graph를 통해 알아보도록 합니다. 위의 그림과 같이 Loss에 대한 W의 Gradient는 Upstream Gradient(dL/df)에 Local Gradient(df/dW)를 통해 구할 수 있습니다. 이때 df/dW는 X와 같습니다. (곱셈에 대한 역전 파는 반대 값을 곱해주는 것과 같기 때문입니다.)
따라서 X의 값이 항상 Positive(+) 라면 dL/dW의 값은 Upstream Gradient(dL/df)의 값에 따라 정해지게 됩니다. 따라서 Gradient W의 값은 항상 Positive 또는 Negative 값이 됩니다. 이 말인즉슨 gradient W는 항상 같은 방향으로 움직인다는 것을 의미합니다.

(X가 항상 Positive라고 가정했을 때) W의 gradient는 항상 Positive 또는 Negative였습니다.
(2차원의 W값이 있다고 가정을 해보겠습니다. x축을 w1, y축을 w2로 가정합니다.)
이때 W의 Update는 w1이 증가했을 때 w2도 증가하는 경우, w1이 감소했을 때 w2도 감소하는 두 가지 경우에 따라 Update 됩니다. (* 왜냐하면 W의 gradient(기울기)가 X가 항상 Positive일 때 항상 Positive or Negative 였기 때문입니다)
그런데 최적의 해가 w1이 증가했을 때 w2는 감소하는 방향입니다.(위의 그래프에서 파란색 직선)
W의 gradient가 항상 Positive or Negative인 경우는 비효율적으로 최적해를 탐색하게 됩니다.
위의 그림과 같이 파란색 직선으로 해를 탐색하는 것이 아닌 'zig zag'로 해를 탐색하게 되는 것입니다. 여러 번 탐색을 해야 하기 때문에 비효율적인 weight update방법이 됩니다.
이것이 바로 우리가 일반적으로 zero-mean data를 원하는 이유입니다.
입력 X가 양수/음수를 모두 가지고 있으면 gradient w가 전부 Positive/Negative로 움직이는 것을 막을 수 있습니다.
02. tanh

- tanh
- 특징
- 출력 값은 -1에서 1로 압축시켜줍니다.
- zero-centerd 합니다(Nice!, sigmoid가 가졌던 두 번째 문제점을 해결해줍니다)
- 단점
- 여전히 gradient가 죽는 구간이 있습니다. (양수/음수 구간 모두 존재합니다)
- 특징
03. ReLU

- ReLU
- 특징
- 양의 값에서는 Saturated 되지 않습니다.
- 계산 효율이 뛰어납니다. sigmid/tanh보다 훨씬 빠릅니다.(6배 정도)
- 생물학적 타당성도 가장 높은 activation function이라고 합니다.
- 단점
- zero-centerd가 아니라는 문제가 다시 발생했습니다.(non-zero centered)
- 또한 음수 영역에서 saturated 되는 문제가 다시 발생합니다.
- 여담
- ImageNet 2012에서 우승한 AlexNet이 사용했습니다.
- 특징
음수 영역에서 다시 Saturated 되는 현상이 나타납니다.

Dead ReLU

ReLU가 DATA CLOUD로부터 떨어져 있을 때 Dead ReLU가 발생할 수 있습니다.
첫째, 초기화를 잘못한 경우입니다.
가중치 평면이 data cloud에서 멀리 떨어져 있는 경우입니다. 이런 경우 어떤 입력 데이터에서도 activate 되지 않습니다.
더 흔한 경우는 Learning rate가 높은 경우입니다.
가중치 파라미터 업데이트의 learning rate가 높은 경우 ReLU가 데이터의 manifold를 벗어나게 됩니다. 이런 일들은 학습과정에서 흔한 일이고 충분히 발생할 수 있다고 합니다.
그래서 학습이 잘 되다가 죽어버리게 된다고 합니다.
Q. 그렇다면 data cloud에서 ReLU가 죽어버리는지 아닌지를 어떻게 알 수 있을까요?
위의 예를 다시 보겠습니다. 간단한 2차원의 예를 통해 알아보도록 하겠습니다. 이때 가중치는 초평면(active ReLU 또는 dead ReLU)을 이루게 될 것입니다.
W의 초평면의 위치와 Data의 위치를 고려했을 때 W의 초평면 자체가 Data와 동떨어지는 경우가 발생할 수 있습니다.

Dead ReLU를 피하기 위해 실제로 ReLU를 초기화할 때 positive biases를 추가해 주는 경우가 있습니다. Weight Update시에 active ReLU가 될 가능성을 조금이라도 늘려주기 위함입니다.
하지만 이 방법이 도움이 된다는 주장도 있고 도움이 되지 않는다는 주장도 있다고 합니다.
04. Leaky ReLU
ReLU 이후에 조금 수정된 버전이 나왔습니다. 그중 하나는 바로 Leaky ReLU입니다.

- Leaky ReLU
- 특징
- ReLU와 유사하지만 negative regime(음의 영역)에서 더 이상 0이 아닙니다.
- saturated 되지 않습니다
- 여전히 계산이 효율적이며 빠릅니다
- 더 이상 Dead ReLU현상이 없게 됩니다
- 특징
05. PReLU
또 다른 예시로는 prametric rectifier, PReLU가 있습니다.

PReLU는 negative space에 기울기가 있다는 점에서 Leaky ReLU와 유사한 것을 알 수 있습니다. 다만 여기에서는 기울기가 alpha라는 파라미터로 결정이 됩니다.
alpha를 딱 정해놓는 것이 아니라 backprop으로 학습시키는 파라미터로 만든 것입니다.
06. ELU
또 하나의 예시로는 Exponential Linear Units(ELU)가 있습니다.

ELU는 LU 패밀리입니다(ReLU, LeakyReLU, PReLU...)
하지만 ELU는 zero-mean에 가까운 출력 값을 보입니다.(그래프를 보시면 0을 기준으로 조금 스무스합니다)
앞선 LU패밀리가 zero-mean 출력 값을 갖지 못하는 것에 비해 상당한 이점을 가지고 있습니다.
하지만 Leaky ReLU와 비교해보면 ELU는 negative에서 "기울기"를 가지는 것 대신에 또다시 "Saturated"되는 문제를 나타냅니다.
ELU는 이런 Saturation이 좀 더 noise에 강인할 수 있다고 주장을 합니다. 이런 deactivation이 좀 더 강인함을 줄 수 있다고 주장합니다. ELU의 논문에는 ELU가 왜 더 뛰어난지 잘 설명을 해준다고 합니다. (시간이 나면 한 번 볼 만하겠군요!)
ELU는 ReLU와 Leaky ReLU의 중간 정도라고 보시면 된다고 합니다. ELU는 Leaky ReLU처럼 zero-mean의 출력을 내지만 Saturation관점에서는 ReLU의 특성도 가지고 있습니다.
Maxout Neuron
끝으로 Maxout Neuron에 대해 알아보겠습니다.

지금까지 본 활성화 함수들과는 조금 다르게 생겼습니다. 입력을 받아들이는 특정한 기본 형식을 미리 정의하지 않습니다.
대신에 w1에 x를 내적 한 값 + b1과 w2에 x를 내적 한 값 +b2의 최댓값을 사용합니다. Maxout은 두 값 중 최댓값을 선택합니다.
Maxout은 ReLU와 Leaky ReLU의 좀 더 일반화된 형태입니다. 왜냐하면 Maxout은 두 개의 선형 함수를 취하기 때문입니다. (ReLU, Leaky ReLU를 보시면 선형 함수 두 개의 결합인 것을 알 수 있습니다)
Maxout 또한 선형이기 때문에 Saturation 되지 않으며 gradient가 죽지 않을 것입니다. 여기서 문제점은 뉴런당 파라미터의 수가 두 배가 된다는 것입니다. 이제는 W1과 W2 두 개의 파라미터를 가지고 있어야 합니다.
TLDR;
Too Long Don't Read

지금까지 다양한 활성화 함수를 살펴보았습니다. 실제로 가장 많이 쓰는 것은 바로 ReLU입니다.
다만 ReLU를 사용하려면 learning rate을 아주 조심스럽게 결정해야 할 것입니다. (Dead ReLU에 빠지면 안 되겠죠?)
learning rate에 관한 내용은 Lecture 6의 후반부에서 더 자세히 다루도록 하겠습니다.
LU 패밀리도 사용을 할 수 있으실 겁니다.
tanh를 사용하면 기대를 별로 안 하시는 게 좋을 것이고
sigmoid는 절대 사용하지 말라고 하네요 ㅎㅎ
이 외에도 최근에는 다양한 Activation들이 연구되고 있습니다. 그 부분은 앞으로 제가 공부를 해 나가면서 필요할 때마다 정리해보도록 하겠습니다.
오늘은 다양한 Activation Function에 대해 알아봤습니다. 내용이 조금 많지만 앞으로 계속해서 사용할 친구들이기에 확실히 짚고 넘어가셨으면 합니다. 긴 글 읽어주셔서 감사합니다. 좋은 하루 보내세요.
참고자료
- cs231n Lecture 6. Training Neural Network Part I
- 투빅스 13기 최혜빈 님의 강의자료
- Wiki Pedia
'Deep Learning > 모두를 위한 cs231n' 카테고리의 다른 글
| [모두를 위한 cs231n] Lecture 6. Training Neural Network - Data Preprocessing (0) | 2020.05.18 |
|---|---|
| [모두를 위한 cs231n] Lecture 6. Weight Initialization (0) | 2020.05.18 |
| [모두를 위한 cs231n] Lecture 8 - Part3. TensorFlow Framework (0) | 2020.05.12 |
| [모두를 위한 cs231n] Lecture 8 - Part2. Deep Learning Framework (0) | 2020.05.11 |
| [모두를 위한 cs231n] Lecture 8 - 개요 (0) | 2020.05.08 |




댓글