Generative Model
AutoEncoder: Background
VAE(Variational AutoEncoder)
- VAE - Intractability
- VAE - Network
- Derive Likelihood & Optimization
Generating Data
Summary

Generative Model

VAE를 학습하기 전에 Generative Model에 대해 짚고 넘어가도록 하겠습니다. Generative Model에 대한 내용은 이원웅 님의 블로그를 참고했습니다.

VAE는 일종의 Generative Model이라고 봐야합니다
Generative Model이란
- training data가 주어졌을 때 이 data가 sampling 된 분포와 같은 분포에서 새로운 sample을 생성하는 model을 말합니다
- 즉 p_model(x)가 최대한 p_data(x)에 가깝게 만드는 것이 목표입니다
- 따라서 얼마나 기존 모델과 가까운 것인가에 대한 지표를 만들어야 하며 그 차이를 최소화하는 방향으로 gradient를 구해 업데이트해야 합니다

오늘 다루는 VAE는 Generative Model 중 Approximate density방법입니다
앞서 간단히 설명했던 Generative Model의 특징을 떠올리며 하나씩 살펴보도록 하겠습니다!

지금까지 배웠던 내용

앞선 chapter에서는 PixelCNN에 대해 배웠습니다
PixelCNN은 tractable density function입니다. 즉 데이터를 통해 최적의 likelihood를 구할 수 있습니다.
반면 앞으로 배우게 될 VAE는 intractable density function입니다.
최적화를 직접적으로 할 수 없기 때문에 lower bound로 유도하여 likelihood를 구해야 합니다.

무슨 말인지 이해가 안 가신다고요?? 하나하나 살펴보도록 하겠습니다.

AutoEncoder: Background

AutoEncoder의 주요 목적은 Dimensionality Reduction입니다

VAE를 배우기 앞서 AutoEncoder부터 알아보도록 하겠습니다.

AutoEncoder란 비지도 학습 방법 중 하나입니다.
AutoEncoder의 주요 목적은 unlabeled training data로부터 lower-dimensional feature representation을 학습하는 것입니다.
그림을 통해 이해하면 보다 직관적으로 이해하실 수 있습니다.

Input data x가 Encoder를 거쳐 lower-dimension으로 표현됩니다. 따라서 dimensionality reduction의 효과를 얻습니다.

그러면 왜 dimensionality reduction을 하는 것일까요?

왜냐하면 우리는 의미 있는 요소들을 가지고 있는 feature를 추출하기 원하기 때문입니다.

* 지금부터 등장하는 Feature, 특징이라는 용어는 같은 의미로 사용됩니다 *

즉 data의 variation을 표현할 수 있는 중요한 feature들을 추출하고 싶은 것입니다.

예를 들어 사람의 얼굴을 잘 나타내는 특징을 추출하기 원한다면 눈을 나타내는 특징, 코를 나타내는 특징, 입을 나타내는 특징 등을 추출하면 되겠죠?? 이처럼 data의 Variation을 잘 표현할 수 있는 중요한 특징들을 추출하는 것이 AutoEncoder의 목적입니다

AutoEncoder는 Encoder에서 Input data를 압축하고 Decoder를 통해 Input data를 복원합니다
Input data를 압축하고 복원하는 과정에서 Input data의 중요 특징을 학습하게 됩니다
학습이 잘 되었는지 확인하기 위해서는 Loss Function이 필요합니다.
위의 예제에서는 L2 Loss function을 사용했습니다

한 가지 주의할 점
- AE에서는 Loss Function을 사용합니다. 하지만 이때 Label이 필요하지 않습니다.
- 즉 레이블 없는 학습 데이터로만 학습합니다.(기억하세요!)

한편 Decoder는 training시 loss계산에서만 사용합니다.
training이 끝난 뒤에는 decoder를 버립니다

이렇게 Encoder를 통해 추출한 특징은 supervised model의 초기값으로 사용됩니다

그럼 여기서 한 번 간단하게 정리해보도록 하겠습니다.

AutoEncoder정리
- AE는 많은 레이블링 되지 않은 데이터로부터 양질의 general feature representation을 학습 가능합니다
- 학습시킨 feature representation을 데이터가 부족한 supervised learning 모델의 초기화 값으로 사용합니다
- AE는 입력값을 복원하는 과정에서 특징(Feature Representation)을 잘 학습하며 학습된 특징은 supervised learning 모델의 초기화에 사용할 수 있습니다.
- 즉 latent vector z가 학습 데이터의 variational을 잘 가지고 있습니다
특히 소량의 데이터로 학습을 해야 하는 경우 feature representation은 더 좋은 특징을 초기화할 수 있도록 도와줍니다.

VAE(Variational AutoEncoder)

이제 VAE(Variational AutoEncoder)에 대해 알아보도록 하겠습니다
우선 한 가지 기억할 점은 AE와 VAE는 이름은 유사하지만 수학적으로는 전혀 관계가 없습니다
그리고 Variational AutoEncoder는 Generative Model이라는 점을 기억하세요!

AutoEncoder와 달리 VAE는 새로운 이미지를 생성합니다
z라는 latent variable을 사용하여 x라는 이미지를 생성하는 모델입니다
마치 AutoEncoder의 decoder처럼 latent vector로부터 이미지를 생성합니다

우리가 VAE를 통해 얻고자 하는 것은 true parameter θ값입니다

이 모델을 표현하기 위해 우리는 p(z)를 가우시안으로 가정합니다
그리고 conditional, p(x|z)을 구하기 위해 Neural Net을 정의합니다

모델을 train 하기 위해서는 FVBN(Fully Visible Brief Network)을 사용합니다
generative model을 training 하는 전략으로 FVBN을 사용한다고 합니다
여기서 우리가 알아야 할 것은 트레이닝 데이터의 Likelihood를 최대화하는 모델의 parameter를 구해야 하는 것입니다
그 과정을 아래서 살펴보도록 하겠습니다

우선 probability density function을 정의합니다
pθ(X)
- 이때 dataset은 X = X(i) 1~N
- datapoint(X(i))는 i.i.d 하다고 가정합니다
pθ(X)는 parameter θ가 정해졌을 때, X라는 데이터가 나올 확률입니다
따라서 이 확률을 최대화하는 것이 Generative model 또는 Density Estimation의 목표입니다

latent vector z를 사용해 pθ(X)를 다시 정의해 보도록 하겠습니다

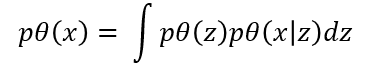
우변 해석
- pθ(z): latent vector z를 sampling 할 수 있는 확률밀도함수입니다
- pθ(x|z): z가 주어졌을 때 x를 생성해내는 확률밀도함수입니다
- 이때 pθ(x|z)는 θ에 대해 미분 가능해야 합니다

VAE - Intractability

하지만 위의 수식은 문제가 있습니다 intractable 합니다
그 이유는 가능한 모든 z에 대해 integral(영어로 적분)을 하기 때문입니다
따라서 직접적으로 미분할 수 없습니다
이 문제를 MLE로 풀기 위해서는 미분 가능한 형태로 만들어줘야 합니다
z를 구성하고 integral 할 수 없는 문제를 VAE가 해결해줍니다

대부분의 z에 대해 pθ(x|z)는 거의 0의 값을 가질 것입니다. 따라서 sampling이 상당히 많이 필요합니다.
좀 더 efficient 하게 sampling을 진행하기 위해 data에 dependent 한 z를 sampling 할 필요가 있습니다
따라서 pθ(z|x)를 생각해 내는 것입니다
pθ(z|x)가 하는 역할은 x가 주어졌을 때 이 x를 생성해 낼 것 같은 z에 대한 확률 분포를 만들어 내는 것입니다.
위와 같이 Baye's Rule을 적용해 쓸 수 있습니다.
하지만 앞서 pθ(x)가 intractable 하기 때문에 pθ(z|x) 또한 intractable 합니다.

그렇다면 문제를 어떻게 해결할 수 있을까요??

Solution
- Decoder network모델링을 위해 추가적인 Encoder Network를 정의해줍니다
  - pθ(z|x)를 근사하는 qϕ(z|x)를 구성합니다
  - ϕ라는 새로운 parameter로 표현되는 qϕ(z|x)는 일종의 Encoder라고 볼 수 있습니다
  - 하지만 원래의 posterior를 approximate 했기 때문에 error가 존재하게 됩니다
  - 따라서 원래의 objective function에 대한 lower bound를 정의해 줘야 합니다

모델이 학습을 어떻게 하고 어떻게 최적화되는지 이어서 살펴보도록 하겠습니다.

VAE Network

결국 VAE에서 하고 싶은 것은 데이터의 확률론적 생성(probabilistic generation) 모델을 만들고 싶은 것입니다
VAE 네트워크 구조를 통해 알아보도록 하겠습니다

VAE네트워크를 통해 학습과정을 살펴보겠습니다
- Encoder는 qϕ(z|x)이며 x를 input으로 받아서 z space상에서 확률분포를 만듭니다
- 이 확률분포는 gaussian이라고 가정해서 만듭니다
- 이 data dependent 한 gaussian 분포로부터 z를 sampling 합니다
- sampling 된 z를 가지고 decoder pθ(x|z)는 x의 space 상의 gaussian distribution 혹은 Bernoulli distribution을 output으로 내놓습니다
- 그러면 x를 이 분포로부터 sampling 할 수 있게 됩니다
- 이러한 구조를 가지기 때문에 Auto-Encoder가 되는 것이며 학습이 되고 나면 latent variable z라는 data의 의미 있는 representation을 얻을 수 있게 되는 것입니다

Derive likelihood

지금부터는 VAE의 Likelihood 유도에 대해 살펴보도록 하겠습니다

우리가 원하는 것은 logpθ(x)를 최대화 시키는 것입니다
유도 공식을 line by line으로 설명해 보겠습니다
- line 1: 우선 log likelihood를 qϕ(z|x)로부터 sampling한 latent vector z에 대한 expectation식으로 바꿔줄 수 있습니다
- line 2: Baye's rule 적용
- line 3: 분모 분자에 qϕ(z|x)을 곱해줍니다
- line 4: log 수식을 정리하면 다음과 같은 식으로 정리할 수 있습니다
- line 5: 수식은 3개의 term으로 정리가 됩니다
Decoder Network Term(첫 번째 term):

[reconstruction]: original input being reconstructed
qϕ(z|x)로부터 sampling한 z를 가지고 pθ(xi|z)가 xi를 생성한 log likelihood

KL term
- prior z(p(z))와 posterior qϕ(z|x)사이의 KL-divergence
- 즉 근사된 posterior의 분포가 얼마나 normal distribution과 가까운지에 대한 척도입니다
- (단 이때 prior를 normal distribution으로 가정)
KL term(마지막 KL term)
- pθ(z|xi)는 intractable하기 때문에 값을 계산하기 어렵습니다 (Intractible: Baye's rule을 적용한 수식(p(z|x))이 계산이 되지 않는 것을 확인)
- 하지만 KL의 성질(특성)에 의해 세번째 항(마지막 KL term)은 무조건 0보다 크거나 같다
따라서 {첫 번째 term과 두 번째 term을} 하나로 묶어주면 원래의 objective function에 대한 tractable한 lower bound를 정할 수 있습니다
MLE 문제를 풀기 위해서는 objective function을 미분해서 gradient ascent를 할 것이며
Lower bound가 정의된다면 이 lower bound를 최대화하는 문제로 바꿔 gradient를 구할 수 있는 것입니다

좀 더 쉽게설명해보겠습니다
- 결국 학습을 위해서는 미분을 하고 gradient(기울기)값을 구해야 하는데 intractable한 pθ(x)를 tractable하게 유도하여 lower bound 문제로 정의해 주는 것입니다
- lower bound인 이유는 첫 번째 term과 두 번째 term의 값의 합 이상으로 MLE를 구해야 하기 때문입니다. (마지막 term은 0이상이니깐!)

아래의 강의 슬라이드를 참고하여 보다 깊은 이해를 하길 바랍니다.

Generating Data

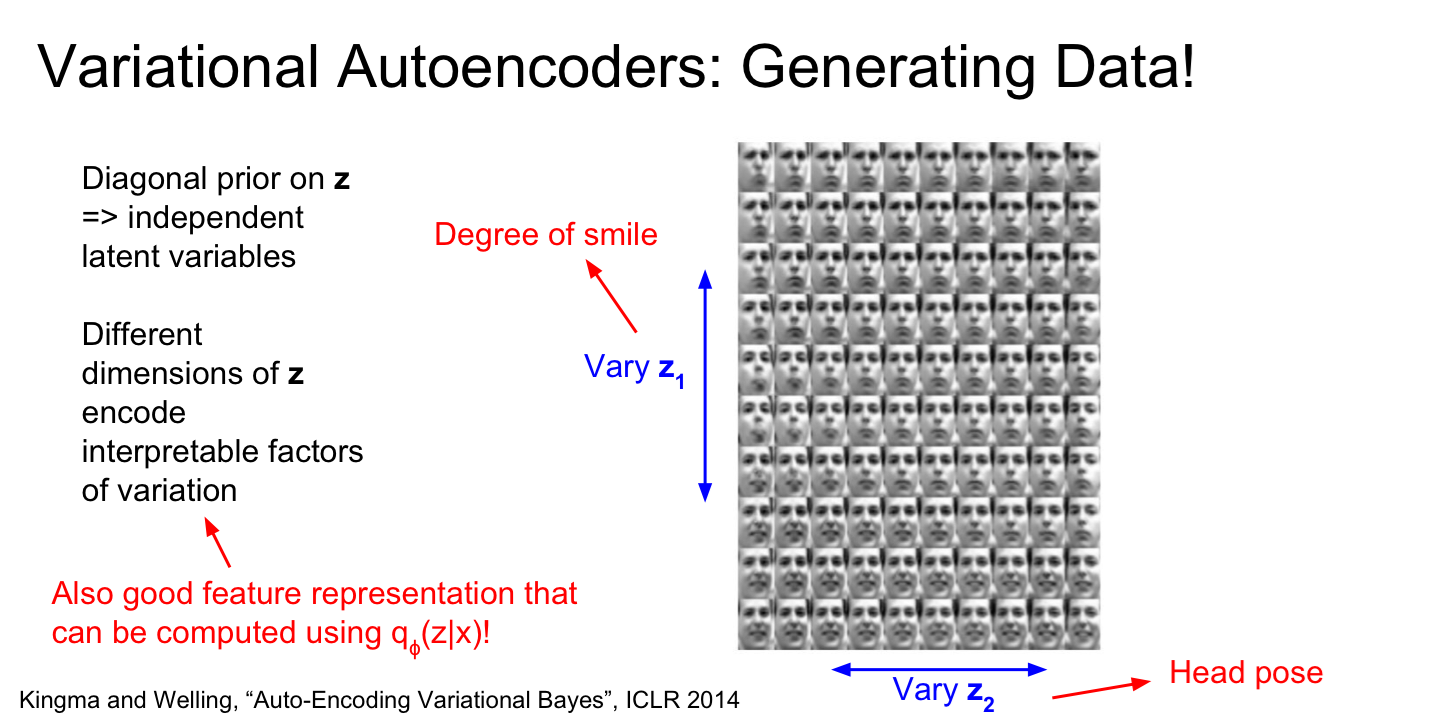
VAE를 통해 Latent Vector z를 학습하면 Data Generating이 가능해집니다
위의 사진처럼 z1과 v2의 값을 조정하여 다양한 값들을 생성해 낼 수 있게 되는 것입니다
데이터의 특징을 잘 담은 feature를 조절하여 이미지를 생성하는 것입니다
위의 사진에서는 z1을 통해 웃는 정도를 조정하며 z2를 통해 얼굴 포즈를 조절할 수 있었습니다
정말 신기하지 않나요??

Summary

지금까지 VAE에 대해 알아봤습니다
VAE를 이해하기 위해서는 VAE가 생성 모델이라는 것을 잊어서는 안됩니다
그리고 수식을 유도하는 과정과 VAE 네트워크의 관계를 파악해보시기를 권장드립니다

지금까지 VAE에 대해 살펴보았습니다. VAE의 개념이 글을 정리하는 지금도 완벽하게 정리되지는 않은 것 같습니다. 포스팅에 오타가 있을 경우 말씀해주신다면 감사하겠습니다. 계속 공부해나가며 부족한 부분들은 채워보도록 하겠습니다. 긴 글 읽어주셔서 감사합니다. 좋은 하루 보내세요! 이상 Steve Lee였습니다

Reference

cs231n 2017 Lecture 13: cs231n syllabus
VAE Tutorial 1: 이원웅 님의 블로그
AutoEncoder의 모든 것: 이활석님의 Naver사내 강의자료

저작자표시 비영리

'Deep Learning > 모두를 위한 cs231n' 카테고리의 다른 글

[모두를 위한 cs231n] Lecture 6. Batch Normalization에 대해 알아보자 (4)	2020.05.19
[모두를 위한 cs231n] Lecture 6. Training Neural Network - Data Preprocessing (0)	2020.05.18
[모두를 위한 cs231n] Lecture 6. Weight Initialization (0)	2020.05.18
[모두를 위한 cs231n] Lecture 6. Activation Functions에 대해 알아보자 (1)	2020.05.18
[모두를 위한 cs231n] Lecture 8 - Part3. TensorFlow Framework (0)	2020.05.12

Steve-Lee's Deep Insight

[모두를 위한 cs231n] Lecture 13 - Part 2. VAE(Variational AutoEncoer)

VAE(Variational AutoEncoder)

모두를 위한 cs231n

Part 2. Index

Generative Model

지금까지 배웠던 내용

AutoEncoder: Background

VAE(Variational AutoEncoder)

VAE - Intractability

VAE Network

Derive likelihood

Generating Data

Summary

Reference

'Deep Learning > 모두를 위한 cs231n' 카테고리의 다른 글

댓글

티스토리툴바

[모두를 위한 cs231n] Lecture 13 - Part 2. VAE(Variational AutoEncoer)

VAE(Variational AutoEncoder)

모두를 위한 cs231n

Part 2. Index

Generative Model

지금까지 배웠던 내용

AutoEncoder: Background

VAE(Variational AutoEncoder)

VAE - Intractability

VAE Network

Derive likelihood

Generating Data

Summary

Reference

'Deep Learning > 모두를 위한 cs231n' 카테고리의 다른 글

관련글

댓글

티스토리툴바