AutoEncoder의 모든 것
본 포스팅은 이활석님의 'AutoEncoder의 모든 것'에 대한 강연 자료를 바탕으로 학습을 하며 정리한 문서입니다. 이활석님의 동의를 받아 출처를 밝히며 강의 자료의 일부를 인용해왔습니다.
AutoEncoder의 모든것
AutoEncoder의 모든것 😀(Last Update 20.07.16.Thur - Chap4. VAE Architecture)
👉🏻 시작합니다! 🎈
Chap0. AutoEncoder란 무엇인가? 핵심만 짚어보자
👉🏻 Deep Neural Network의 학습방법 📗
- Backpropagation과 MLE
Chap1. Deep Neural Network의 학습 방법에 대해 알아보자(딥러닝 학습방법)😃
👉🏻 Manifold Learning이란 무엇인가? 📑
- Manifold Learning 및 Dimensionality Reduction에 대해 알아보자
Chap2. Manifold Learning이란 무엇인가
👉🏻 AutoEncoder 탐구하기 ⌛️
Chap3. AutoEncoder란 무엇인가(feat. 자세히 알아보자)
👉🏻 Variational AutoEncoder에 대해 알아보자 ☕️
Chap4. Variational AutoEncoder란 무엇인가(feat. 자세히 알아보자)
👉🏻 VAE 파생 모델에 대해 알아보자
- Conditional VAE, Adversarial AutoEncoder에 대해 알아보자
Chap4. VAE Architecture - Conditional VAE, Adversarial AutoEncoder
[정리노트] [AutoEncoder의 모든것] Chap3. AutoEncoder란 무엇인가(feat. 자세히 알아보자)
AutoEncoder의 모든 것 본 포스팅은 이활석님의 'AutoEncoder의 모든 것'에 대한 강연 자료를 바탕으로 학습을 하며 정리한 문서입니다. 이활석님의 동의를 받아 출처를 밝히며 강의 자료의 일부를 인�
deepinsight.tistory.com
안녕하세요 Steve-Lee입니다. 앞서 Chap 3. 에서는 AutoEncoder에 대해 살펴보았습니다. 이번 시간에는 Variational AutoEncoder에 대해 알아보도록 하겠습니다.
강연자이신 이활석님께서는 '사실 앞에서 다뤘던 내용들은 모두 Variational AutoEncoder를 설명하기 위함'이라고 하셨습니다. 다시 말해 우리가 주목해야 할 Chapter는 바로 'Chapter 4 - Variational AutoEncoder'가 아닌가 생각합니다.
(Chap1, Chap2, Chap3의 내용들은 Variational AutoEncoder를 설명하기 위한 배경지식을 쌓는 과정이 아니었을 까요?)
그럼 Chap4. Variational AutoEncoder 시작하겠습니다.
Prologue
Chap4는 수식이 많아서 딱 주무시기 좋아요
-네... 저도... 많이 졸았었습니다...
VAE를 처음 제대로 공부해야겠다고 마음먹었을 때 제가 봤던 영상이 바로 AutoEncoder의 모든 것입니다. Chap4. Variational AutoEncoder 영상을 틀고 10분 뒤 졸고 있는 제 자신을 발견했었죠...ㅎㅎ
강연자 이활석님의 말씀처럼 Chap4를 처음 들었을 때 잠이 미친 듯이 몰려왔습니다... 소귀에 경 읽기였을까요... 화려한 수식과 방대한 내용들은 제 귀에 한 편의 아름다운 자장가로 들려왔었습니다...(죄송합니다 이 명 강의를....!! ㅠㅠ)
이번 포스팅을 통해 Variational AutoEncoder의 기본과 핵심을 다시 정리하며 향후 연구에서 AutoEncoder를 활용할 수 있는 기반을 잘 닦고 싶습니다.
※ Chap4는 수식이 많아 강의 슬라이드를 매우 많이 인용해 왔습니다. ※
강의 슬라이드는 이곳에서 받으실 수 있습니다.
그럼 시작하겠습니다!
Generative Model이란 무엇인가?
Variational AutoEncoder는 Generative Model입니다. 잠깐, Generative Model이란 무엇일까요?
단어에 내포된 의미를 해석해보면 '무언가를 생성'해주는 모델이라는 느낌을 받을 수 있습니다. 구글링을 해보면 Google Developer에서는 Generative Model에 대해 다음과 같이 설명합니다.
- Generative model can generate new data instance. // 새로운 data instance를 생성할 수 있다
- Discriminative models discriminate between different kinds of data instanes. // Discriminative model은 data instance를 종류에 따라 나눌 수 있다
- Generative models capture the joint probability p(X, Y), or just p(X) if there are no labels. // Generative models은 확률분포를 포착합니다.
Generative Model이란 결국 새로운 data instance를 생성해내는 모델입니다.
단어 그대로 '생성'을 하는 특성을 가지고 있는 모델인 것이죠. 그리고 여기서 '생성'이란 단순히 Data Instance를 생성하는 것이 아닌 Training Data의 distribution을 근사하는 특성을 가지고 있습니다.
예를 들어 고양이, 강아지의 이미지 데이터를 Generative Model의 입력으로 준다면 우리는 입력 데이터와 상당히 유사한 분포(distribution)를 갖는 새로운 이미지를 얻게 됩니다. Deep Learning Model 중 널리 알려진 Generative Model로는 GAN 모델을 들 수 있겠네요.

이번 시간에 다룰 Variational AutoEncoder(이하 VAE로 표기)도 Generative Model의 일종입니다. 그리고 여기서 한 가지 짚고 넘어가야 할 점이 있습니다. 바로 'VAE와 AE는 전혀 관계가 없다는 점입니다'
수학적으로 AutoEncoder와 Variational AutoEncoder는 전혀 관계가 없습니다.
정리하면
- AutoEncoder의 목적은 Manifold Learning입니다
- AE는 네트워크의 앞단을 학습하기 위해 뒷단을 붙인 것입니다
- 입력 데이터의 압축을 통해 데이터의 의미있는 manifold를 학습합니다
- Variational AutoEncoder는 Generative Model입니다
- 뒷단(Decoder, 생성)을 학습시키기 위해 앞단을 붙인 것입니다
- 그런데 공교롭게도 그 구조를 보니 AE와 같은 것입니다
- VAE는 Generative Model입니다. 기억하세요!

저는 VAE라는 표현이 너무나도 재미있는 표현이라고 생각합니다.
몇 가지 주요 키워드들을 살펴봤습니다.
#생성모델, #확률분포, #AutoEncoder
이제 VAE의 학습과정을 하나씩 배우면서 어떤 특징이 있는지 살펴보도록 하겠습니다!
Again, AE는 Manifold Learning, VAE는 Generative Model.
두 모델은 단지 이름과 모양만 비슷합니다!
Viewpoint1. Generative Model

우선 VAE를 Generative Model관점에서 살펴보도록 하겠습니다. VAE가 최종적으로 원하는 것은 무엇일까요??
앞서 말했듯이 고양이와 강아지 데이터가 있다면 기존에 Training DB에 가지고 있던 고양이, 강아지와 유사한 샘플을 생성해 내는 것이 목적일 것입니다. 이를 조금 더 추상화시켜볼까요?
결국 VAE 네트워크가 학습을 통해 출력하고자 하는 결과는 Training DB에 있는 데이터 x가 나올 확률을 구하는 것이 목적입니다.
우리는 VAE 네트워크의 출력 값을 우리가 정한 모델에 대한 파라미터의 MLE(Maximum Likelihood Estimation) 값을 통해 구할 것입니다. 그리고 한 가지 더 살펴볼 점이 있습니다.
단순히 샘플을 생성해내는 것이 아닌 컨트롤러(controller)로 생성된 이미지를 조정을 할 수 있다면 어떨까요?
VAE 네트워크를 살펴보면 Generator는 Latent Variable z로부터 샘플을 생성합니다. 이때 마치 controller처럼 이미지를 조정하는 z vector를 추출할 수 있다면 어떨까요? 고양이에 귀여움을 조절하여 귀여운 고양이를 생성하는 상상을 할 수 있을까요??
이처럼 VAE 네트워크의 z vector(이하 Latent Vector로 정의하겠습니다)는 controller의 역할을 하게 됩니다.
- 정리
- VAE는 Generative Model이다
- z vector로 생성되는 이미지를 controller 할 수 있다
단 두 문장을 설명하기 위해 장황하게 표현했네요...ㅎㅎ 하지만 이런 그림을 가지고 하나씩 다가가면 이해하는데 도움이 되리라 생각합니다.
Prior Distribution p(z)
기존 Training DB에 있던 샘플과 유사한 샘플을 생성하기 위해서 우리는 prior값을 활용합니다.
여기서 잠깐,
Q1. 만약 prior값이 normal distribution값을 띈다고 가정하고 sampling을 한다면 sampling 된 값은 manifold를 대표하는 값을 가질 수 있을까요?
정답은 Yes입니다. (제겐 조금 신기한 부분이었습니다.)
학습을 수행하는 네트워크가 Deep Neural Network이기 때문에 가능하다고 합니다. Network의 앞 단에 있는 한, 두 개의 layer는 manifold를 잘 찾기 위한 역할을 수행할 수 있다고 합니다.
즉 한, 두 개의 layer가 복잡한 latent space를 익히는 데 사용될 수 있다고 합니다. 따라서 prior distribution으로 간단한 distribution(e.g normal distribution)을 해도 걱정하지 않으셔도 됩니다.
아래의 슬라이드에는 그 내용이 보다 자세히 적혀 있습니다...!

Q2. 그렇다면 MLE를 직접적으로 사용하면 되지 않을까요?
📌 MLE를 direct로 사용하면 되지 않는 이유를 아는 것이 VAE를 이해하는 길입니다

한 가지 가정을 해보겠습니다.
- 우리는 p(x|g𝜃(z))의 likelihood 값이 높기를 원합니다.
생성기(Generator)에 대한 확률 모델을 가우시안으로 할 경우, MSE관점에서 더 가까운 것이 더 p(x)에 기여하는 바가 크게 됩니다. MSE가 더 작은 이미지가 의미적으로는 더 가까운 경우가 아닌 이미지들이 많기 때문에 현실적으로 올바른 확률 값을 구하기는 어렵습니다.
예를 들면 좀 더 직관적으로 다가옵니다.
위의 슬라이드에서 (a)에서 일부가 잘린 데이터가 (b), (a)의 화소 값을 조금 옮긴 값을 (c)라고 가정해봅니다. 의미론적으로는 (a)와 (c)의 값이 더 유사하지만 MSE를 구하면 (a)와 (c)의 MSE(Mean Square Error) 값이 더 큽니다.
이처럼 MSE가 더 작은 이미지가 의미적으로 더 가까운 경우가 아닌 이미지들이 많기 때문에 prior에서 sampling을 하게 되면 문제가 발생하게 되는 것입니다.
그래서 등장한 방법이 바로 Variational Inference입니다.
Variational AutoEncoder

이제는 prior에서 sampling 하는 것이 아닌 이상적인 sampling함수를 통해 samplilng을 수행합니다. 그리고 우리가 원하는 결과는 네트워크의 출력 값이 x와 가까워지는 것입니다. 이를 위해 다음의 3-step을 밟습니다.
Step 1. 의미론적으로 가까운 sample들을 생성시키는 z 정의
Step 2. z를 생성할 수 있는 이상적인 sampling 함수 정의
Step 3. x를 given으로 주어 학습을 수행
x를 보여줄 테니 적어도 x를 잘 generate 하는 이상적인 sampling함수를 생각해봐!
p(z|x)가 아닌 이상적인 sampling함수인 qΦ(z|x)를 추정하고 이상적인 sampling함수가 정의되었다면 z vector로부터 Input x와 유사한 데이터를 생성할 수 있게 됩니다.
그런데 우리는 그 이상적인 sampling함수를 모르기 때문에 Variational Inference(변분 추론)을 사용합니다.
Variational Inference
- True posterior: 우리가 추정하고자 하는 확률분포
- Approximation class: 우리가 다루기 쉬운 확률 분포(e.g Gaussian, Bernulli)
- Gaussian일 경우 확률분포를 결정짓는 파라미터 μ와 𝜎를 추정
- Φ를 잘 바꿔가며 True posterior를 추정(Approximation)
- 학습이 잘 될 경우, True posterior를 잘 approximation 하는 함수를 가지고 z생성
- 생성된 z를 통해 sample을 생성(x는 잘 나오겠지!)
- term 정리
- true posterior: p(z|x) - how likely the latent variable is given the input
- prior: p(z) - how the latent variables are distributed without any conditioning
- approximation function(sampling function): q(z|x)
한번 정리하고 가겠습니다.
- 학습이 잘 되기 위한 z sample을 잘 만들어 내는 함수가 있었으면 좋겠다
- Variational Inference 방법으로 확률 분포중에 Target Distribution을 잘 나타내는 Distribution을 찾는다
- e.g) 확률분포를 Gaussian으로 정한다면 μ와 𝜎를 추정 → 추정된 값을 통해 Approximation
- 잘 찾은 z로부터 Sampling을 해서 Generator를 생성하면 잘 될 것 같다
이제는 Variational AutoEncoder의 학습과정을 수식으로 알아보도록 하겠습니다. 위의 가정들이 수식에 어떻게 녹아들어 있는지 생각해보면서 본다면 도움이 될 것이라 생각합니다.
ELBO(Evidence LowerBOund)
자 그러면 이제 그 유명한 ELBO를 찾아 한 번 떠나보겠습니다.
결론부터 말하자면 우리가 찾기 원하는 값은 p(x) 값을 최적화시킨 값입니다.
✅ 우리가 원하는 것은 Training DB에 있는 input data와 유사한 분포를 갖는 값을 갖기를 원하는 거예요! ← 계속 반복됩니다
p(x)의 최댓값을 구하기 위해서 log값을 씌워줄 수 있고 log(p(x))값은 다음과 같이 전개가 됩니다.

log(p(x))값을 정리하면 우리는 ELBO(Φ) 값과 KL(qΦ(z|x)||p(z|x))값을 얻게 됩니다.
결과적으로 우리가 원하는 것은 log(p(x)) 값의 최적화이기 때문에 EBLO(Φ) + KL에서 ELBO(Φ)의 값을 최적화합니다.
KL은 두 확률 분포(qΦ(z|x)와 p(z|x)) 사이의 거리로 0 이상의 값을 가집니다. 이 수식은 계산이 불가능하기 때문에 ELBO(Φ)를 최대화하는 문제로 해결하는 것입니다.
두 확률분포 간의 거리는 항상 0 이상이기 때문에 최적 화식은 ELBO term 이상의 값이 됩니다. 때문에 우리는 최적화 식을 Evidence Lower BOund 'ELBO'라고 합니다.
한편 우리는 각각의 term이 의미하는 것을 이해할 수 있어야 합니다.
- ELBO(Φ)
- KL(qΦ(z|x)||p(z|x))
이를 위해 ELBO 수식을 조금 더 전개해 보도록 하겠습니다.
ELBO를 계산해보자

ELBO 수식을 전개해보면 EqΦ(z|x)[log(p(x|z))] - KL(qΦ(z|x)||p(z))의 수식을 얻게 됩니다. (KL term이 하나 더 보이네요?? 당황하지 않으셔도 됩니다)
슬라이드 7의 수식과 연계해보면 다음의 최종 수식을 얻을 수 있습니다.

수식에서 중요한 것은 각 term이 무엇을 의미하는지 이해하는 것입니다.

앞서 슬라이드 7에서 두 확률분포 간의 거리인 KL term은 계산을 할 수 없기에 앞에 ELBO를 최적화시켜줘야 한다고 언급했습니다. 따라서 우리가 최적화를 시켜야 할 값은 'Reconstruction term'과 'Regularization term'입니다.
결론적으로 다음의 수식을 최적화하는 문제로 정의할 수 있게 됩니다.


VAE 우리가 너에게 바라는 점은 두 가지야.
첫 째, 이상적인 샘플링 함수로 부터 생성한 z값으로부터 (Training DB에 있는) input data와 유사한 데이터를 생성해줘 ← Generattion
둘 째, 이상적인 sampling함수의 값이 최대한 prior값과 같도록 만들어줘 ← Condition
ELBO 정리하기
마지막으로 ELBO 수식을 정리해보도록 하겠습니다.
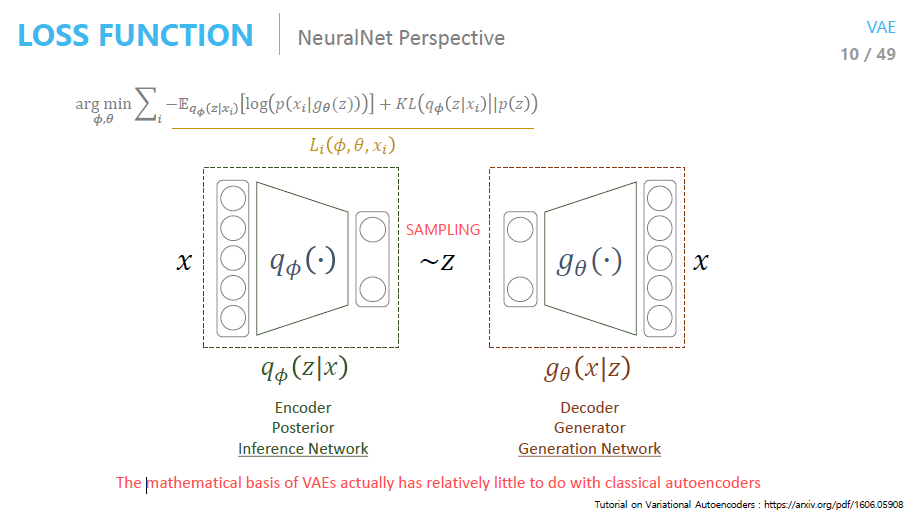
지금까지 배웠던 내용을 다시 한번 정리해 보겠습니다.
결국 우리의 목적은 Generator를 학습시키는 것입니다.(VAE는 generative model이라고 했죠?)
그런데 prior만 가지고 학습을 시키면 학습이 잘 되지 않기 때문에 우리는 이상적인 sampling 함수를 도입하는 것입니다.
이상적인 sampling 함수는 바로 qΦ(z|x)입니다.
x를 evidence로 주고, x에 대해서 Generator가 잘 학습할 수 있도록 만들어주는 z를 sampling 하기 위해서 qΦ(z|x)를 도입한 것입니다.
그리고 sampling 한 값이 input값과 같아줬으면 하기 때문에(Reconstruction Term), 𝜃를 최적화시키는 MLE문제로 풀 수 있습니다.
↑위의 키워드들이 연결이 되시나요?! 반복해서 읽어보시길 바랍니다!
<결론>
- ELBO term을 Φ에 대해 maximize 하면 이상적인 sampling함수를 찾는 것이다
- ELBO term을 𝜃에 대해 maximize 하면 MLE 관점에서 Network의 파라미터를 찾는 것이다

Reparameterization Trick
한 가지 주의할 점은 Sampling과정에서 Backprop을 진행할 때 문제가 발생한다는 점입니다.
아래 슬라이드와 같이 'Reparameterization Trick'을 사용하면 Backpropagation이 가능하도록 도와줍니다.
(수학적으로 증명이 되었기에 사용하시면 됩니다)

Summary

Training DB에 있는 Input data와 비슷한 분포를 가지는 데이터를 생성(Generate!) 하기 위해 우리는 이상적인 sampling함수를 도입했습니다.(바로 qΦ(z|x)!)
Gaussian 확률분포를 따르는 이상적인 sampling 함수로부터 z를 sampling 합니다. 이때 계산을 위해 'reparameterization trick'을 사용해 sapling의 term과 𝜎를 곱해주고 여기에 𝜇값을 더해줍니다.
학습 과정으로는 ELBO term을 Φ에 대해 maximize 하면 이상적인 sampling함수를 찾는 것이며 ELBO term을 𝜃에 대해 maximize 하면 MLE 관점에서 Network의 파라미터를 찾는 것입니다.
이때 Training DB에 있는 Input Data와 비슷하게 복원되어야 한다는 조건(condition)은 'reconstruction term'에 녹아있고, reconstruction이 잘 된 이상적인 sampling함수의 z값이 prior(p(z))와 같았면 좋겠다는 조건(condition)을 'regularization term'에 녹여주면 되는 것입니다.
AutoEncoder와 Variational AutoEncoder
그렇다면 AutoEncoder로 학습한 것과 Variational AutoEncoder로 학습했을 때 가장 큰 차이는 무엇일까요?
결론부터 말씀드리면 AutoEncoder는 'prior에 대한 조건(Condition)'이 없기 때문에 의미있는 z vector의 space가 계속해서 바뀌게 됩니다. 즉 새로운 이미지를 생성할 때 z 값이 계속해서 바뀌게 됩니다.
반면 Variational AutoEncoder의 경우 prior에 대한 Condition을 부여했기 때문에 z vector가 prior과 같은 분포를 따릅니다. e.g prior가 Normal distribution이라면 z vector도 같은 분포를 갖는다.
따라서 prior에서 sampling을 하면 됩니다.


VAE를 통해 학습이 잘 되었다면 z값을 2D공간에 투영을 시켰을 때 같은 데이터들에 대해서는 z값이 뭉쳐지고 다른 데이터들은 흩어지게 됩니다.
그리고 오른쪽 그림과 같이 z vector는 데이터의 중요한 특성들을 담고 있죠!
어떤 데이터인지, 두께, 로테이션이 어떻게 되는지를 단 2개의 vector로 표현하고 있답니다. 정말 멋지군요.
마치며
지금까지 우리는 Generative Model 중 하나인 VAE에 대해 배워보았습니다.
처음 VAE를 공부할 때는 개념의 이해부터 최적화 수식까지 머릿속이 복잡하기만 했었는데 정리하고 또 정리하면서 조금씩 개념이 잡혀가는 것 같습니다.
생성 모델이라는 점에서 너무나도 흥미롭고 이후 어떤 연구들이 진행되었는지 궁금해지네요.
다음 시간에는 Variational AutoEncoder Architecture들에 대해 살펴보도록 하겠습니다. Conditional VAE, Adversarial VAE 등에 대해 다뤄보도록 하겠습니다.
제 포스팅이 조금이나마 도움이 되셨으면 좋겠습니다. 이상 Steve-Lee였습니다. 감사합니다!




댓글