Manifold Learning이란 무엇인가
본 포스팅은 이활석님의 'AutoEncoder의 모든 것'에 대한 강연 자료를 바탕으로 학습을 하며 정리한 문서입니다. 이활석님의 동의를 받아 출처를 밝히며 강의 자료의 일부를 인용해왔습니다.
AutoEncoder의 모든것 (포스팅 리스트)
AutoEncoder의 모든것 😀(Last Update 20.07.16.Thur - Chap4. VAE Architecture
👉🏻 시작합니다! 🎈
Chap0. AutoEncoder란 무엇인가? 핵심만 짚어보자
👉🏻 Deep Neural Network의 학습방법 📗
- Backpropagation과 MLE
Chap1. Deep Neural Network의 학습 방법에 대해 알아보자(딥러닝 학습방법)😃
👉🏻 Manifold Learning이란 무엇인가? 📑
- Manifold Learning 및 Dimensionality Reduction에 대해 알아보자
Chap2. Manifold Learning이란 무엇인가
👉🏻 AutoEncoder 탐구하기 ⌛️
Chap3. AutoEncoder란 무엇인가(feat. 자세히 알아보자)
👉🏻 Variational AutoEncoder에 대해 알아보자 ☕️
Chap4. Variational AutoEncoder란 무엇인가(feat. 자세히 알아보자)
👉🏻 VAE 파생 모델에 대해 알아보자
- Conditional VAE, Adversarial AutoEncoder에 대해 알아보자
Chap4. VAE Architecture - Conditional VAE, Adversarial AutoEncoder
지난 시간에는 Deep Neural Network의 학습 방법에 대해 알아보았습니다.
Deep Neural Network의 학습 방법이 MLE와 같다는 것에 대한 이해가 있으시다면 Chap2를 시작하셔도 좋습니다.
만약 이 말에 의미가 와닿지 않으신다면 아래의 포스팅을 참고해 주시길 바랍니다.
AutoEncoder의 모든것 Chap1. Deep Neural Network의 학습 방법에 대해 알아보자
What is AutoEncoder? 본 포스팅은 이활석님의 'AutoEncoder의 모든 것'에 대한 강연 자료를 바탕으로 학습을 하며 정리한 문서입니다. 이활석님의 동의를 받아 출처를 밝히며 강의 자료의 일부를 인용해�
deepinsight.tistory.com
Manifold Learning
우선 Manifold Learning에 대해 직관적으로 알아보도록 하겠습니다.
Manifold란 고차원 데이터(e.g Image의 경우 (256, 256, 3) or...)가 있을 때 고차원 데이터를 데이터 공간에 뿌리면 sample들을 잘 아우르는 subspace가 있을 것이라는 가정에서 학습을 진행하는 방법입니다.
이렇게 찾은 manifold는 데이터의 차원을 축소시킬 수 있습니다.
✔️Check Slide -> more information about it

- f(·): embedding function
- m: extrinsic dimension
- d: intrinsic dimension or latent space(지금부터 우리는 latent space라는 표현을 많이 사용 할 것입니다!)
Manifold Learning은 언제 사용될까?
manifold Learning이 어디에 사용되는지 물으면 4가지 답을 얻을 수 있습니다.
1. Data Compression
2. Data Visualization
3. Curse of dimensionality
4. Discovering most important features
여기서 3번 차원의 저주를 잠깐 알아보도록 하겠습니다. 강의에서 설명해 주신 내용을 정리해 보도록 하겠습니다.

- 데이터의 차원이 증가할수록 해당 공간의 크기(부피)는 기하급수적으로 증가합니다
- 동일한 개수의 데이터의 밀도는 차원이 증가할수록 급속도로 희박해지게 됩니다
- 따라서 차원이 증가할수록 데이터 분포 분석 또는 모델 추정에 필요한 샘플 데이터의 개수가 기하급수적으로 증가하게 됩니다.
Manifold의 가정

왜 차원의 저주(Curse of Dimensionality)가 Manifold의 특징인지 다음 슬라이드를 통해 알 수 있습니다.
- 고차원의 데이터는 밀도가 낮지만 이를 포함하는 저차원의 매니폴드가 있습니다.
- 이 저차원의 매니폴드를 벗어나는 순간 밀도는 급격히 낮아지게 됩니다.
즉 고차원의 데이터를 잘 표현하는 manifold를 통해 우리는 샘플 데이터의 특징을 파악할 수 있는 것입니다.
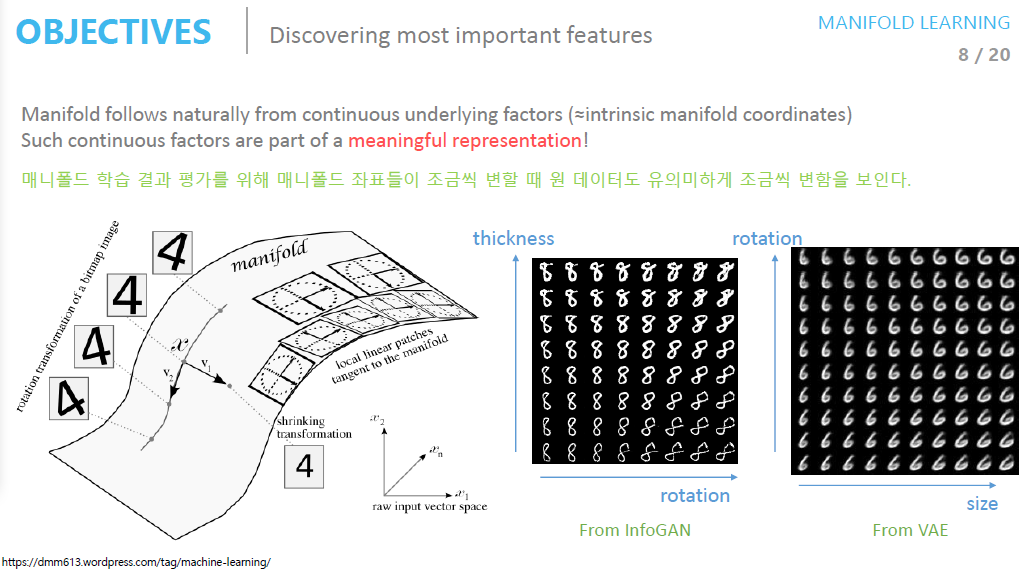
- 앞서 manifold는 고차원 데이터를 잘 표현한다고 배웠습니다
- 고차원의 데이터를 잘 표현한다 함은 바로 데이터의 중요한 특징을 발견하는 것입니다
- 고차원 데이터의 manifold 좌표들을 조정해보면 manifold의 변화에 따라 학습 데이터도 유의미하게 조금씩 변하는 것을 확인할 수 있습니다.

Data(샘플)를 잘 아우르는 manifold를 찾게 되면 어떤 효과를 얻을 수 있을까요?
- Feature를 잘 찾았기 때문에 manifold의 좌표를 조금씩 변경해가면서 데이터를 유의미하게 조금씩 변화시킬 수 있습니다.
- 이는 Data(샘플)의 Dominant 한 Feature를 잘 찾았기 때문입니다.
- 역으로 manifold를 잘 찾았다면 dominant feature가 유사한 sample들을 찾아볼 수 있습니다

- 일반적으로 학습된 manifold는 얽혀 있습니다 (예 : 복잡한 방식으로 데이터 공간에 인코딩 됨)
- manifold 가 풀리면 해석이 쉽고 작업에 쉽게 적용할 수 있습니다.
Dimensionality Reduction Taxonomy

Machine Learning에 대해 공부를 해보셨다면 PCA 알고리즘을 한 번쯤 들어보셨을 것입니다. 간단하게 말하자면 원 데이터를 공간에 뿌려 hyper plane을 찾는 방법입니다. 이때 PCA 알고리즘의 수식은 우리가 Neural Network에서 사용하는 Linear 한 수식이 됩니다. 이 때문에 Taxonomy에서는 Linear 한 방법으로 분류됩니다.
다음 시간부터 다룰 AutoEncoder는 Non-Linear 한 방법론입니다. 벌써부터 기대가 되는군요!
Summary
이번 시간에는 Manifold 및 Manifold Learning에 대해 배워보았습니다.
아마 'AutoEncoder의 모든것' 강의를 통틀어 조금은 숨통이 트이는 시간이 아니었나 생각합니다.
원본 데이터로부터 Dominant한 Feature를 추출하는 Manifold Learning에 대한 개념을 숙지하시길 바랍니다.
이상 Steve-Lee였습니다. 오늘도 감사합니다!
Reference
- AutoEncoder의 모든 것 강의 슬라이드
- AutoEncoder의 모든것 강의
- math.stackexchange: manifold learning: How should this method be interpreted?
'Deep Learning > 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| [정리노트] [AutoEncoder의 모든것] Chap3. AutoEncoder란 무엇인가(feat. 자세히 알아보자) (6) | 2020.07.12 |
|---|---|
| [정리노트] [AutoEncoder의 모든것] Chap 0. AutoEncoder란 무엇인가? 핵심만 짚어보자 (0) | 2020.07.12 |
| [정리노트] AutoEncoder의 모든것 Chap1. Deep Neural Network의 학습 방법에 대해 알아보자(딥러닝 학습방법) (7) | 2020.07.11 |
| [Deep Learning] Bottleneck 현상이란 무엇인가? (0) | 2020.05.08 |
| [Deep Learning] NVIDIA CUDA란 무엇인가? (1) | 2020.05.08 |




댓글