AutoEncoder의 모든 것
본 포스팅은 이활석님의 'AutoEncoder의 모든 것'에대한 강연 자료를 바탕으로 학습을 하며 정리한 문서입니다. 이활석님의 동의를 받아 출처를 밝히며 강의 자료의 일부를 인용해왔습니다.
AutoEncoder의 모든것(포스팅 리스트)
AutoEncoder의 모든것 😀(Last Update 20.07.16.Thur - Chap4. VAE Architecture)
👉🏻 시작합니다! 🎈
Chap0. AutoEncoder란 무엇인가? 핵심만 짚어보자
👉🏻 Deep Neural Network의 학습방법 📗
- Backpropagation과 MLE
Chap1. Deep Neural Network의 학습 방법에 대해 알아보자(딥러닝 학습방법)😃
👉🏻 Manifold Learning이란 무엇인가? 📑
- Manifold Learning 및 Dimensionality Reduction에 대해 알아보자
Chap2. Manifold Learning이란 무엇인가
👉🏻 AutoEncoder 탐구하기 ⌛️
Chap3. AutoEncoder란 무엇인가(feat. 자세히 알아보자)
👉🏻 Variational AutoEncoder에 대해 알아보자 ☕️
Chap4. Variational AutoEncoder란 무엇인가(feat. 자세히 알아보자)
👉🏻 VAE 파생 모델에 대해 알아보자
- Conditional VAE, Adversarial AutoEncoder에 대해 알아보자
Chap4. VAE Architecture - Conditional VAE, Adversarial AutoEncoder
Chap1. Revisit Deep Neural Networks
- 이번 장에서는 Deep Neural Network의 학습 방법에 대해 알아봅니다
- 핵심은 Deep Neural Network가 학습할 때 Loss Fucntion을 해석하는 두 가지 관점의 차이를 이해하는 것입니다
- 두 가지 관점이란 Backpropagation과 MLE입니다
결론적으로...!
Deep Neural Network가 학습하는 것을 해석할 때 이게 MLE구나를 이해하면 이번 Chapter는 성공입니다
Deep Neural Network가 MLE구나?!
아! Deep Neural Network가 학습하는 방식이 MLE구나!!
그럼 Chap1. Deep Neural Network의 학습방법 시작하겠습니다!
01. Machine Learning의 학습 방법

일반적인 Machine Learning의 분류 학습은 다음의 절차로 진행됩니다.
내가 그래도 머신러닝 모델링은 좀 해봤어 싶으시다면 건너 뛰어도 좋을 것 같습니다.
- 입력, 출력 데이터
- 모델 정의
- 모델의 파라미터 학습: 모델을 결정짓는 theta(θ)를 결정
- 출력값과 target(정답)과의 차이를 정의
- 최적의 파라미터 서치
- 최적 함수의 출력 계산
학습과정에 대해서 좀 더 알아보면
모델 학습을 통한 모델을 결정짓는 θ(parameter)를 결정하고, 모델의 출력 값과 target(정답)과의 차이를 통해 최적의 파라미터를 서치 합니다. 그리고 학습을 통해 결정된 최적의 함숫값에 대한 출력을 계산하면서 학습의 결과를 확인할 수 있습니다.
좋은 모델이란 주어진 데이터를 가장 잘 설명하는 모델이어야합니다.
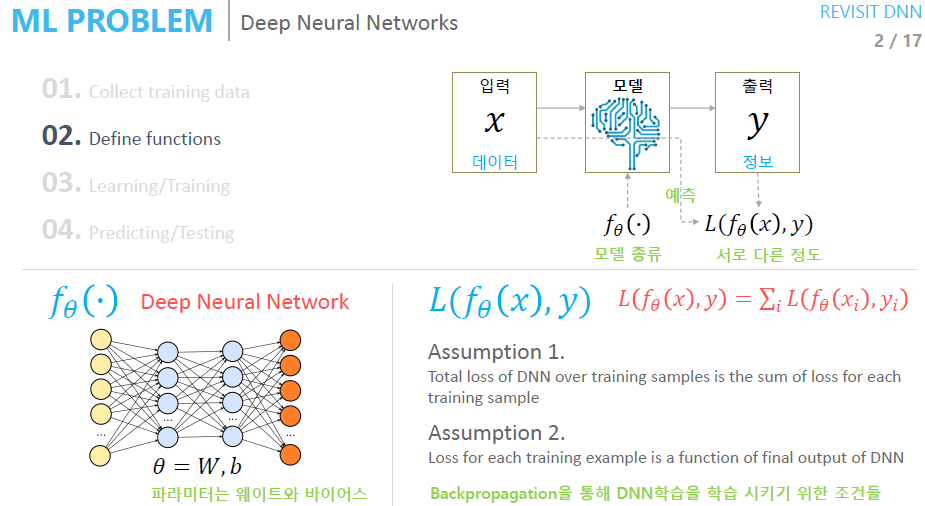
Deep Neural Network의 학습에 대해 좀 더 알아보겠습니다.
Training data가 준비되고 Model이 준비된다면 Loss Function을 정의해줘야 합니다. 이때 우리가 일반적으로 사용하는 Loss Function은 한정적이기 때문에 2가지 가정을 해야 합니다.
- Training data 전체 Loss Function은 각 Loss에 대한 합이다.
- Network 출력 값과 타겟값에 대한 Loss를 구한다.
Backpropagation Algorithm을 적용하기 위해서는 일반적으로 위의 두 가지의 가정을 가정합니다.
-
정리
-
모델을 정해준 다음에 Loss Function을 정해줘야 한다
-
이때 우리가 일반적으로 사용하는 Loss Function은 한정적이다(Cross Entropy 또는 MSE냐)
-
2개의 가정(Assumption)을 기억하자(중요)
- Training data 전체의 loss function은 각각의 loss에 대한 합이다
- Network 출력 값과 타켓값에 대해서 loss를 구한다
⇒ Back prop Algorithm을 적용하기 위해 일반적으로 위의 두 가정을 가정한다
-
01-1. Gradient Descent
그렇다면 이제 Gradient Descent 방법에 대해 알아보겠습니다.
Gradient Descent 방법은 경사 하강법입니다. 산의 정상에서 눈을 가린 채 비탈길을 내려오는 것을 가정해보겠습니다. 현재의 높이가 이동 전의 높이보다 낮다면 더 낮은 지점으로 이동을 하는 알고리즘이 바로 Gradient Descent방법입니다.
Loss Function의 출력값과 모델의 Parameter가 있을 때, Gradient Descent Algorithm을 활용해 최적의 해를 구할 수 있습니다.
Gradient Descent 방법에 대한 직관은 다음과 같습니다.
- Gradient Descent Method
- 현재 θ에서 loss가 줄기만 한다면 loss를 바꾼다
- 현재 θ와 다음 theta의 loss가 같다면 학습을 멈춘다
- 이렇게 경사를 타고 내려가면서 최적해를 탐색하는 것이다
Gradient Descent 알고리즘은 다음과 같습니다.


- Gradient Descent는 다음과 같이 업데이트를 합니다(중요)
- Taylor Expansion → 여기서 1차 미분 값만 쓸 거야
- Approximation → 근사할 거야
우리가 원하는 것은 loss function이 줄어드는 것입니다. Approximation으로 접근해보겠습니다.
'아~ 우리가 Loss Function에서 Learning rate를 매우 작게 해서 학습을 시키는 이유가 여기에 있었구나!'
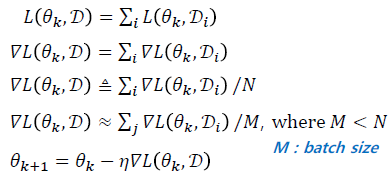
다시 remind 해보면
전체 데이터에 대한 Loss Function 값은 각각의 데이터에 대한 Loss Function의 합으로 가정한다.
그리고 위의 수식을 다시 보면...
- 전체 데이터에 대한 Loss Function 값은 각각의 데이터에 대한 Loss 값의 합이다.
- Loss Function의 기울기는 각각의 Loss Function에 대한 기울기의 합과 같다.
- ...
- 빅데이터로 갈수록 연산량이 많아지기 때문에 전체 데이터에 대해 업데이트를 하는 방식이 아닌 한 Step에 한 번 학습을 하는 방법을 취한다
그럼 이제 Backpropagation 알고리즘의 유도방법에 대해 알아보겠습니다.
그리고 재차 강조하면 이번 Chapter의 핵심은 바로 Deep Neural Network의 학습방법과 MLE가 같다는 것입니다!
Again, Deep Neural Network와 MLE 학습하는 방법이 같네!!
같네?! → 같네!!
'Deep Neural Network와 MLE의 학습 방법이 같다고?!'
'Deep Neural Network와 MLE의 학습 방법이 같다고!!'
지금까지는 일반적인 Deep Neural Network의 학습 방법에 대해 알아보았습니다.
지금부터는 Deep Neural Network의 두 가지 학습방법에 대해 알아보도록 하겠습니다.
View point 1. Backpropagation 알고리즘

Deep Neural Network의 학습에서는 Loss Function의 미분 값이 가장 중요합니다.
Backpropagation 알고리즘에서 미분이 어떻게 활용되는지 이해해보도록 하겠습니다.

- 맨 마지막 단(모델의 맨 끝 지점) Error Signal
- Cost(Loss)를 마지막 output값으로 미분한 값 *(Elementwise) activation 미분값
- 각 레이어 별 Error Signal...
결국 레이어의 종단에서 흐르는 Gradient값에 local gradient를 곱하는 식으로 Gradient가 뒤에서부터 전달되는 것을 알 수 있습니다. Gradient Descent에 대한 자세한 내용은 이곳에서 확인할 수 있습니다.
Backpropagation type 1 - MSE 관점
관점을 심어줄게요. 어떤 Loss Function 사용할래요?
지금 우리는 Deep Neural Network를 학습하는 2가지 방법 중 첫 번째 방법인 Backpropagation 방법에 대해 배우고 있습니다.
우선 MSE 관점에서 Backpropagation을 살펴보도록 하겠습니다.
Mean Square? Cross Entropy?
Q. Backprop관점에서 Mean Square가 좋을까 Cross Entropy가 좋을까?
우선 Mean Square Error 관점부터 살펴보도록 하겠습니다(a.k.a MSE)
간단한 네트워크로 한 번 생각해보겠습니다.
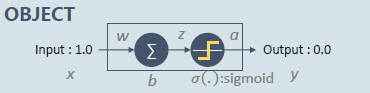
이 네트워크를 학습시키면 어떤 결과를 얻을 수 있을까요?
학습 결과를 살펴보면 학습 결과가 다른 것을 확인할 수 있습니다.
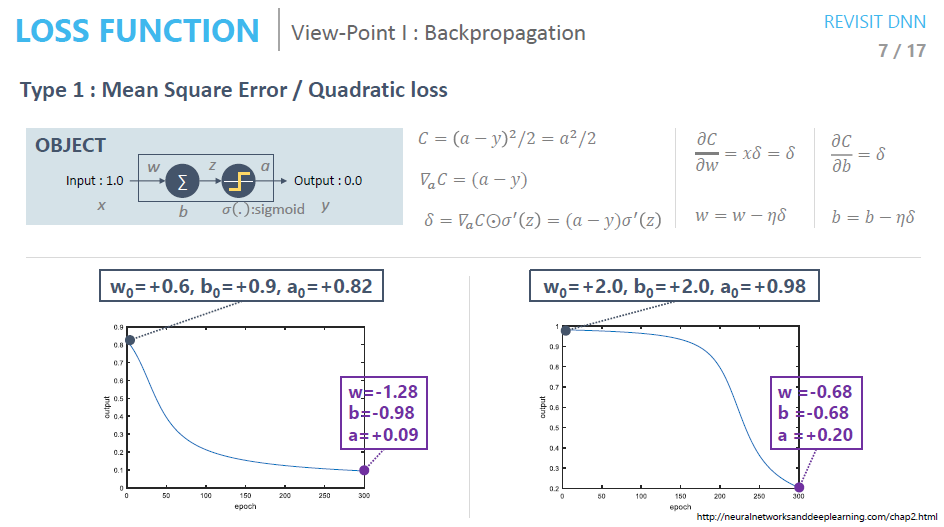
학습 속도가 빠른 것과 느린 것의 차이는 무엇일까요?!
Q. One-Neural Network를 구성해서 학습을 시켰는데 왜 학습 결과가 다를까요?
오른쪽 아래의 Loss값보다 왼쪽 아래의 Loss값이 훨씬 더 빠르게 수렴하는 것을 볼 수 있습니다.
왜 다른 걸까?? 왜??
⇒ 결국엔 초기값이 달라서 그런 것입니다
✅ Back propagation 관점에서 살펴보자 ← 계속해서 반복됩니다. Backpropagation 관점!
⇒ Sigmoid의 미분 값이 0에 가까울 때와 조금 더 클 때의 차이
⇒ 이 point가 중요합니다. Sigmoid 미분 값에 대해 한 번 생각해보겠습니다. cs231n Lecture6의 Activation Function과도 연관됩니다(참고하시면 좋아요)
어떤 Activation Function을 쓰는지 그리고 해당 Activation Function이 Backpropagation에서 어떻게 동작하는지 생각해볼 필요가 있습니다.
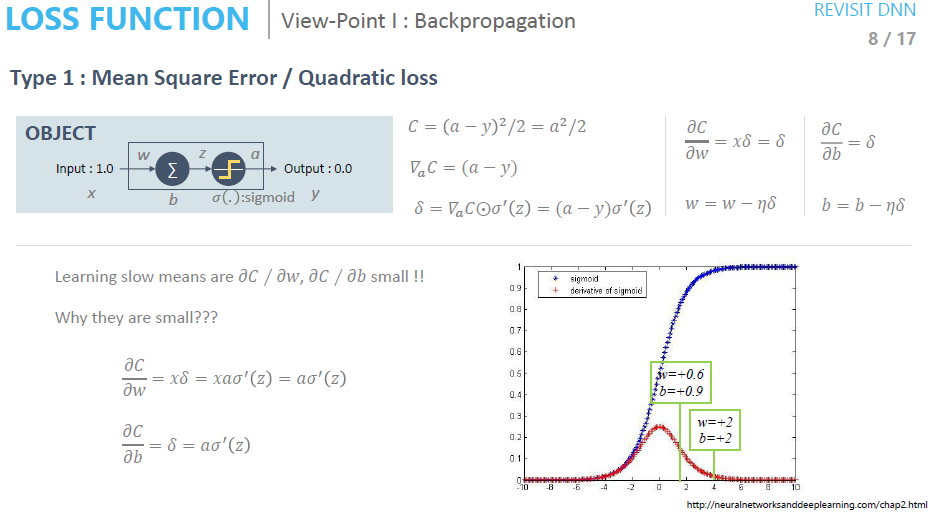
⇒ 두 그래프의 Activation Function 미분 값을 보면 w가 0.6b가 0.9일 때의 미분 값은 약 0.15 정도 되는 것을 볼 수 있습니다. 반면 w가 2, b가 2일 때는 미분 값이 약 0.01로 차이가 큰 것을 알 수 있습니다. 이는 Backpropagation시 전파되는 gradient의 크기가 그만큼 줄어드는 것을 의미합니다.
... ← 1*0.15*0.15 ←1*0.15 ←1
... ← 1*0.01*0.01 ← 1*0.01 ← 1
위와 같이 미분값이 작으면 작을수록 네트워크의 뒷단에서 앞단으로 전파되는 gradient는 점점 작아지게 될 것 입니다. (Gradient Vanishing 현상이라고도 합니다)
그렇게 된다면 눈 가린 채 산에서 내려오는 과정에서 아주 쪼금 발을 아래로 디디게 되겠죠?
Backpropagation type 2 - Cross Entropy 관점

결론부터 말하면 MSE와 달리 CE(Cross Entropy)에서는 출력 레이어에서의 Error값에 대한 activation function의 미분 값이 곱해지지 않아 gradient vanishing problem에서 좀 더 자유로워집니다.
그러나 Layer가 여러 개 사용될 경우에는 결국 activation function의 미분 값이 계속해서 곱해지게 되 gradient vanishing problem에서 완전히 자유로워 질수는 없다고 합니다.

⇒ Question. CE에서 레이어가 여러개 사용될 경우 결국 activation fuction의 미분값이 계속해서 곱해지므로 gradient vanishing problem에서 완전히 자유로울 수는 없다고?!
CE의 미분 값의 경우 출력 레이어에서 (a-y)가 아니었는가?
레이어를 쌓아도 결국은 (a-y)(a-y)... 이렇게 되는 거 아닌가?
activation function의 미분 값이 곱해지는 것이 아니라 activation 값이 곱해지는 거 아닌가?
❌ ⇒ 이 부분에 대한 이해가 완전히 가지는 않는다..,ㅠ 조금 더 찾아보도록 하겠습니다...
🙏 ⇒ 혹시라도 답을 아시는 분이 계신다면 댓글 달아주시길 바랍니다...!

- Quadratic(MSE)에 비해 학습이 더 빨리 되는 것을 알 수 있다.
어떻게 해서 학습이 더 빨리 되는 걸까?
⇒ How?? Why?? -20.07.11.Sat-
Activation Function의 미분값이 곱해지지 않아 gradient가 더 잘 흘러서 그런게 아닐까?
View point 2. Maximum Likelihood 알고리즘 유도방법

똑같은 얘기를 다르게 해석해보자
⇒ Cross Entropy || Maximum Likelihood
확률분포에 대한 likelihood 값이 Maximize 됐으면 합니다.(확률적 관점 해석)
- 확률분포에 대한 가정을 하고 학습을 시작한다.
- Gaussian으로 할게요. 표준편차는 얼마......
- 평균값이 Given 되었을 때 확률 P(y|f(x))
- 평균하고 y값이 같아질 때 학습을 멈춘다
그러니깐 Loss Function은 말이야... Network의 출력과 정답이 가깝길 바라. 이 것을 확률적 관점으로 해석할 것인가 차이로 해석할 것인가 그 차이라고!
- 확률적 관점으로 해석 or 차이(정답-출력 간 차이)로 해석할 것인가

- MLE를 통해 최적의 파라미터 theta(θ)를 찾았다
- 학습을 해서 찾은 값은 Gaussian 확률 분포에 대한 평균을 찾은 것이다(확률분포 모델을 찾은 것이다)
- 이렇게 학습을 하게 되면 '확률분포'를 찾은 것이기 때문에 Sampling을 할 수 있다.
⇒ Sampling을 할 수 있다는 것이 가장 큰 장점입니다.
⇒ 뒤에서 배울 VAE에 대한 뼈대가 될 것입니다.
- i.i.d Condition
- Independence: All of our data is independent of each other
- Identical Distribution: Our data is identically distributed

수식을 정리해보면 다음과 같은 재미있는 사실을 발견할 수 있습니다.
-
Gaussian Loss를 minimize 하는 것은 Mean Square Error와 같다
-
Bernoulli distribution을 minimize 하는 것은 Cross-entropy와 같다
-
Continuous 한 value에 대해서는 Gaussian distribution을 사용
-
Classification과 같은 value에 대해서는 Cross-entropy를 사용
⇒ 철학적으로 그렇다는 것입니다. 항상 정답은 아니라고 하네요
마지막으로 활석님께서 갓이라고 칭하는 Bengio's Slide를 보고 마치도록 하겠습니다.
지금까지 다뤘던 내용을 단 한 장의 슬라이드로 정리해 주셨습니다...ㄷㄷ

이 내용들이 이해가 되어야 VAE를 이해할 수 있다고 합니다.
평균값이 given(주어졌을 때) 확률. 기억하세요!
Summaray
Chap1. 에서 중요한 것은 역시 계속 강조했던 그것과 같습니다.
Neural Network의 학습 방법과 MLE의 학습 방법이 같다는 것입니다.
Neural Network의 최적해 학습 방법 Backpropagation이 정답과 출력 값의 차이를 기준으로 Network를 학습시킨다면 MLE방법에서는 확률적인 관점으로 Network를 학습시킨다는 것입니다.
📌 정리 📌
- Network의 출력과 정답이 가깝기를 바랍니다
- 차이로 해석할 것인가
- 확률적 관점으로 해석할 것인가

뒤에서 다룰 VAE(Variational AutoEncoder)파트에서 VAE 모델의 학습방법을 이해하는데 도움이 되리라 생각합니다.
너무나도 좋은 강의와 강의자료에 다시 한번 감사를 표합니다.
이상 Steve-Lee였습니다!
Reference
'Deep Learning > 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| [정리노트] [AutoEncoder의 모든것] Chap 0. AutoEncoder란 무엇인가? 핵심만 짚어보자 (0) | 2020.07.12 |
|---|---|
| [정리노트] [AutoEncoder의 모든것] Chap2. Manifold Learning이란 무엇인가 (2) | 2020.07.11 |
| [Deep Learning] Bottleneck 현상이란 무엇인가? (0) | 2020.05.08 |
| [Deep Learning] NVIDIA CUDA란 무엇인가? (1) | 2020.05.08 |
| 파이토치(PyTorch)-3.Neural Network 구현하기 (0) | 2020.02.21 |





댓글